기술자료
[솔리드웍스Tip&Tech] 수식 유도 곡선을 이용한 Hyperbolic Paraboloid 모델링

수식 유도 곡선을 이용한 Hyperbolic Paraboloid 모델링
SOLIDWORKS에서 방정식을 스케치 선으로 그려 모델링을 할 수 있을까요?
네 가능합니다.
스케치의 기능인 ‘수식 유도 곡선’을 사용하여 원하는 범위 내의 그래프를 그릴 수 있습니다.
이 기능을 이용해 X축 방향으로는 +Z방향으로 휘어 있고 Y축 방향으로는 -Z방향으로 휜 Hyperbolic Paraboloid,(Saddle) 형상을 모델링 해보겠습니다.
완성본 모델도 함께 첨부하였으니 참고해 보시기 바랍니다.
(SOLIDWORKS 2022 버전으로 제작되어 해당 버전, 혹은 상위버전에서 확인하실 수 있습니다!)
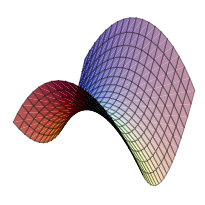
zc=x2a2−y2b2
1. 평면 정의
정면, 윗면, 우측면을 클릭 후 f2를 눌러 각각 YZ, XY, ZX평면으로 이름을 변경합니다.
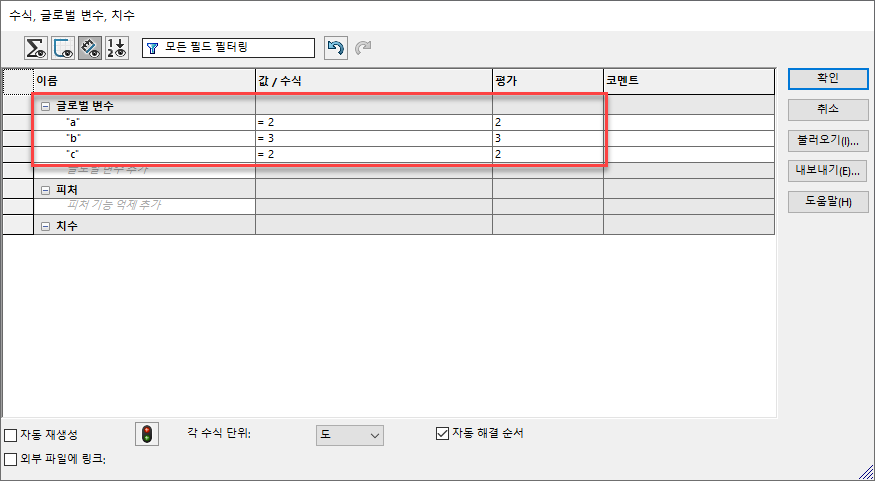
2. 글로벌 변수 생성 (a=2, b=3, c=2)
도구 > 수식을 클릭해
zc=x2a2−y2b2에서 상수 a, b, c의 임의의 값을 지정합니다.결과적으로
z2=x222−y232 인 Hyperbolic Paraboloid곡면을 모델링합니다.
TIP : |
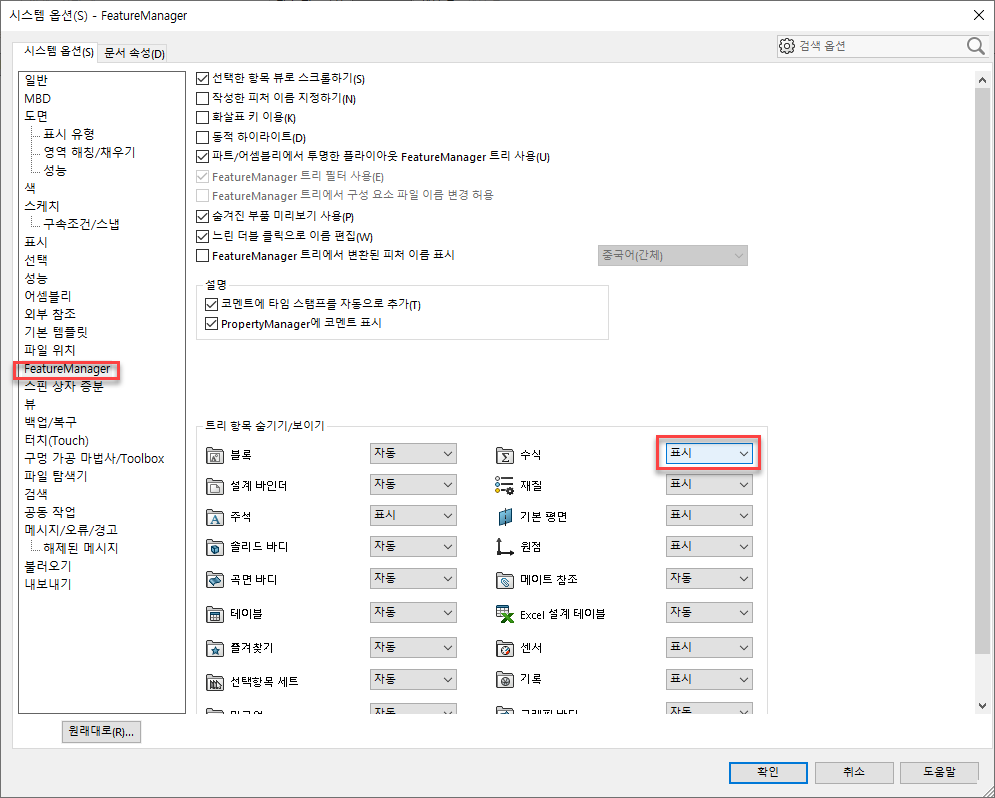
| 시스템 옵션 > FeatureManager > 수식-표시를 설정해 놓으면 FeatureManager에서 바로 수식 접근이 가능합니다. |
3. x=3인 YZ평면 작성
YZ평면을 클릭 후 참조형상 > 기준면을 클릭해 3mm떨어진 면을 생성합니다.
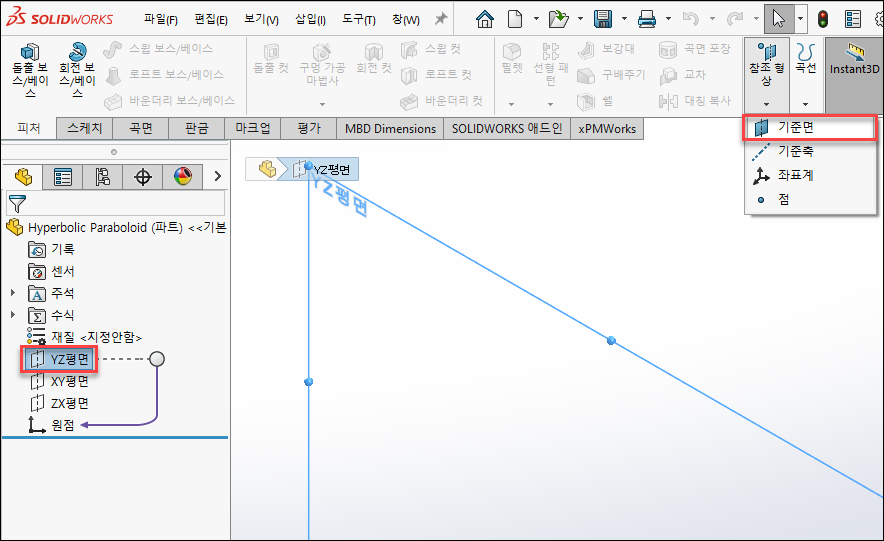
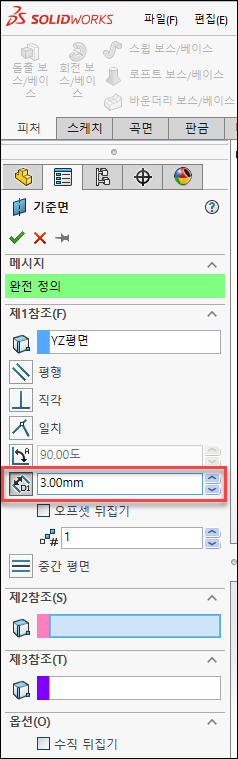
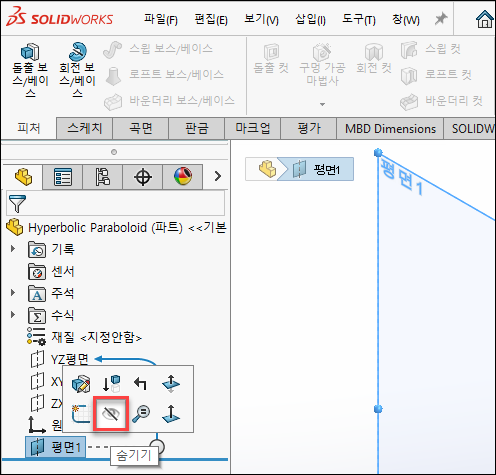
생성된 평면은 숨기기 합니다
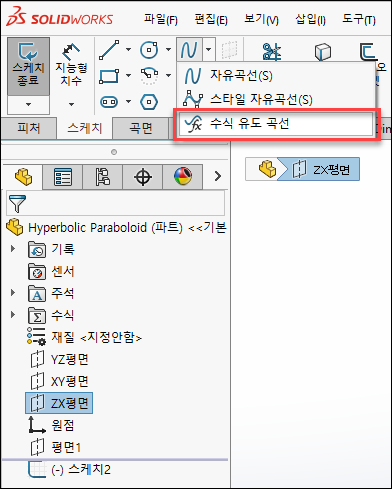
4. ZX 평면 (y=0) 에 스케치 작성
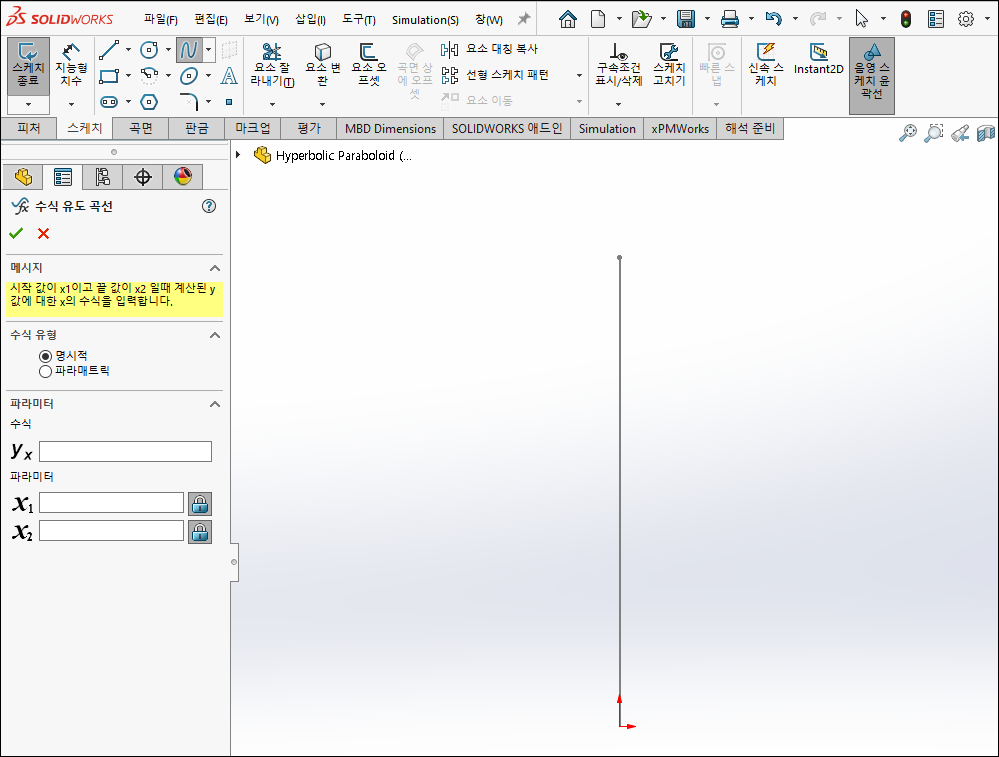
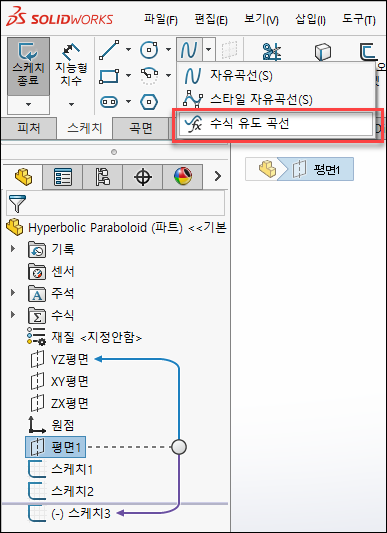
ZX평면을 클릭 후 스케치를 클릭 후, 수식 유도 곡선을 선택합니다.
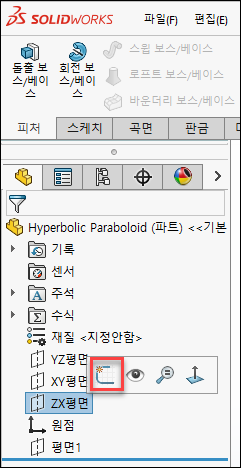
4.1 수식 유도 곡선기능 분석
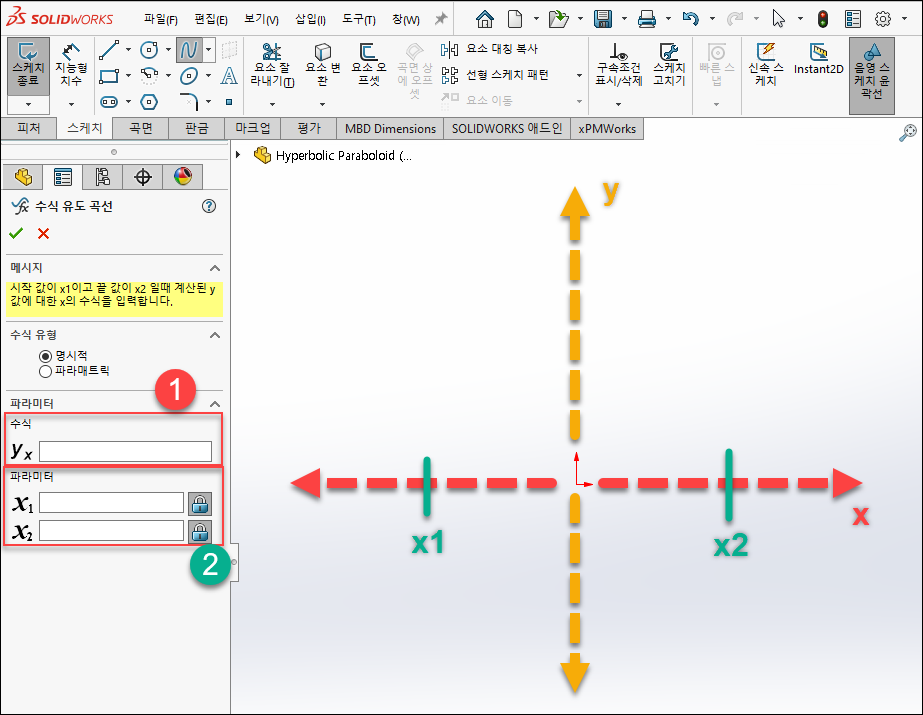
ZX평면상에 원점을 기준으로 x, y축이 있고  수식 칸에 x와 y에 대한 방정식을 작성할 수 있습니다.
수식 칸에 x와 y에 대한 방정식을 작성할 수 있습니다.
 파라미터는 x에 대한 범위를 지정할 수 있습니다.
파라미터는 x에 대한 범위를 지정할 수 있습니다.
4.2 방정식 작성
$\frac{z}{2}=\frac{x^2}{\combi{2}^2}-\frac{\combi{y}^2}{\combi{3}^2}에서\ y=0\ 인경우\ z=2\times \frac{x^2}{\combi{2}^2}\ 이고\ 변수로\ 변환하면\ z=c\times \frac{x^2}{\combi{a}^2}\ 입니다.$z=2×x222이고 변수로 변환하면 z=c×x2a2 입니다.
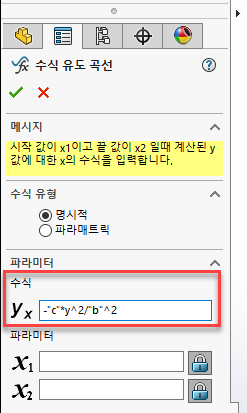
또 z=c×x2a2을 SOLIDWORKS 수식으로 나타내면 z="c"*x^2/"a"^2 입니다.
이 수식을 수식 유도 곡선의 수식 란에 작성합니다.
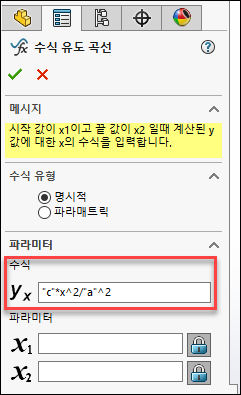
| TIP : "a"와 "c"는 앞선 글로벌 변수로 작성했던 a, c의 값을 불러옵니다. |
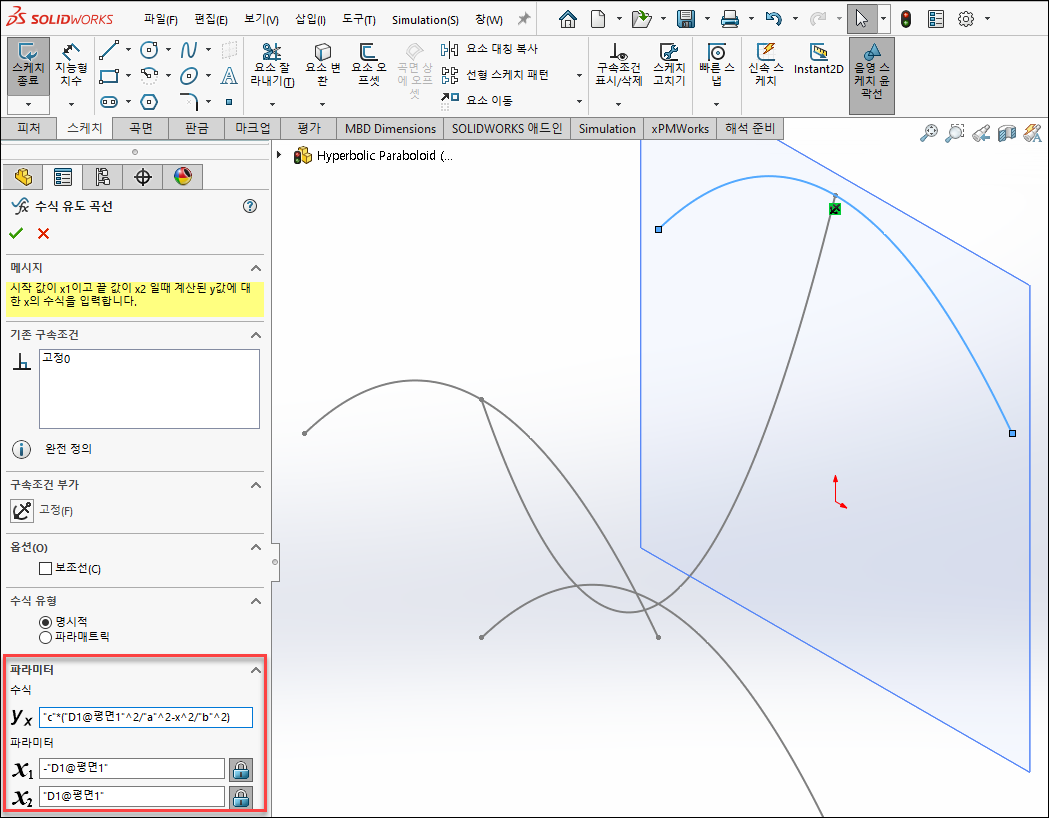
4.3 파라미터(x의 범위) 작성
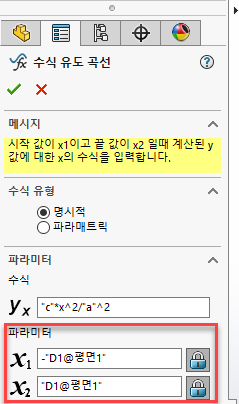
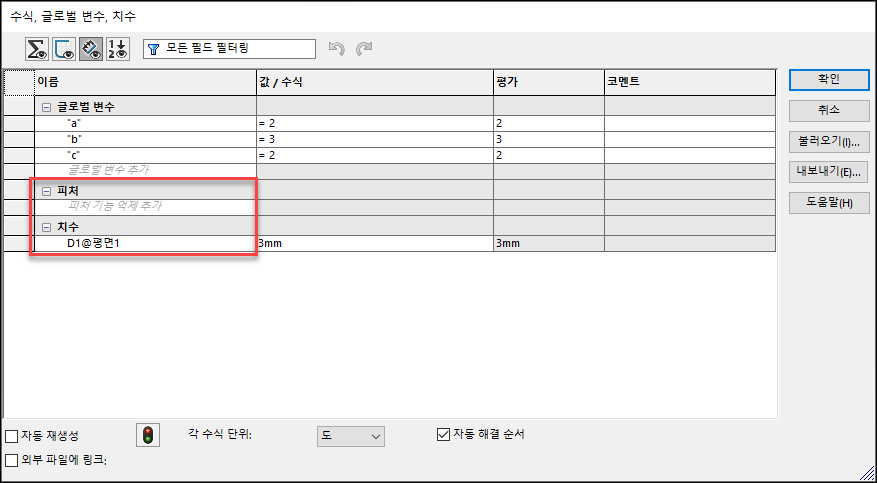
“D1@평면1”의 의미는 ③에서 x=3인 YZ평면을 만들 때 작성한 치수(3mm)입니다.
즉 작성한 파라미터의 의미는 x의 범위가 -3에서 +3까지 입니다.
4.4 수식 유도 곡선 작성
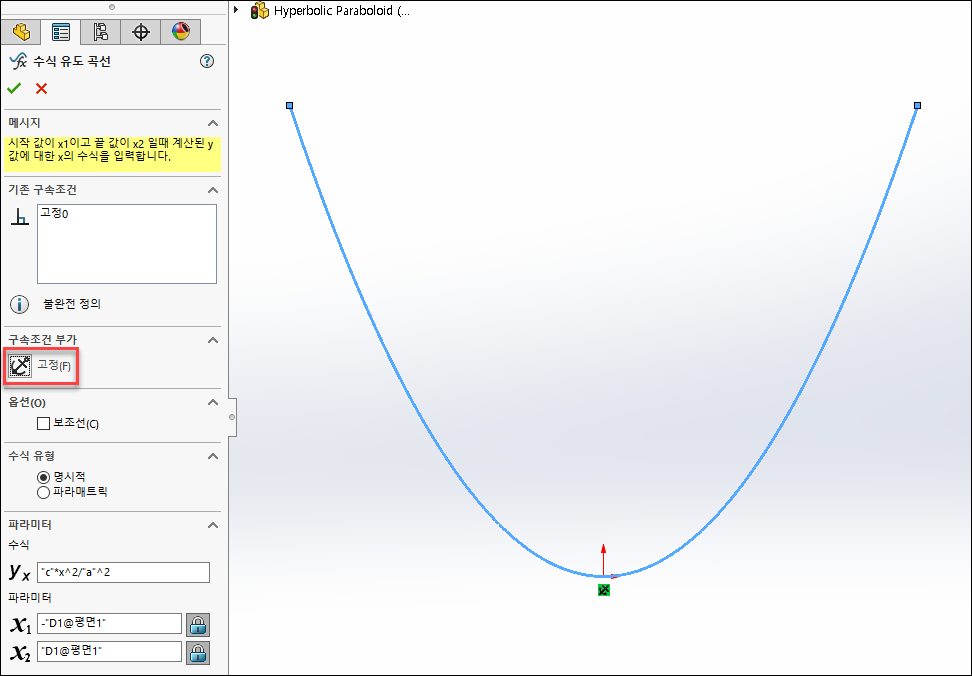
수식과 파라미터를 모두 입력 후 확인을 누른 다음 다시한번 스케치 선을 클릭 후 고정 구속조건을 부가합니다.
TIP : "D1@평면1"과 같이 스케치나 피처에 사용한 치수이름 찾는 방법 1) FeatureManager트리에서 수식 마우스 오른클릭 > 수식관리 2) 피처, 치수란에 사용한 치수 이름 확인 |
5. YZ평면(x=0)에 스케치 작성
위의 4항목을 반복합니다. YZ평면 클릭 후 스케치 > 수식 유도 곡선을 선택
5.1 방정식 작성
에서 x=0인 경우 z=−2×y232 이고 변수로 변환하면 z=−c×y2b2 입니다.
또 z=−c×y2b2을 SOLIDWORKS 수식으로 나타내면 z=-"c"*x^2/"b"^2 입니다..
이 수식을 수식 유도 곡선의 수식 란에 작성합니다.
5.2 파라미터(x의 범위) 작성
위의 4.3에서 작성했던 x의 범위를 기입합니다.
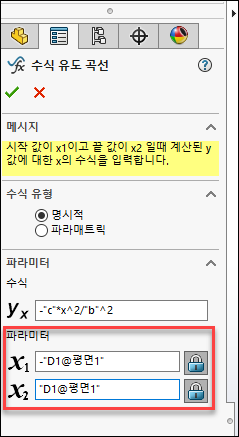
5.3 수식 유도 곡선 작성
수식과 파라미터를 모두 작성 후 확인을 누르고 스케치 선을 클릭 후 고정 구속조건을 부가합니다.
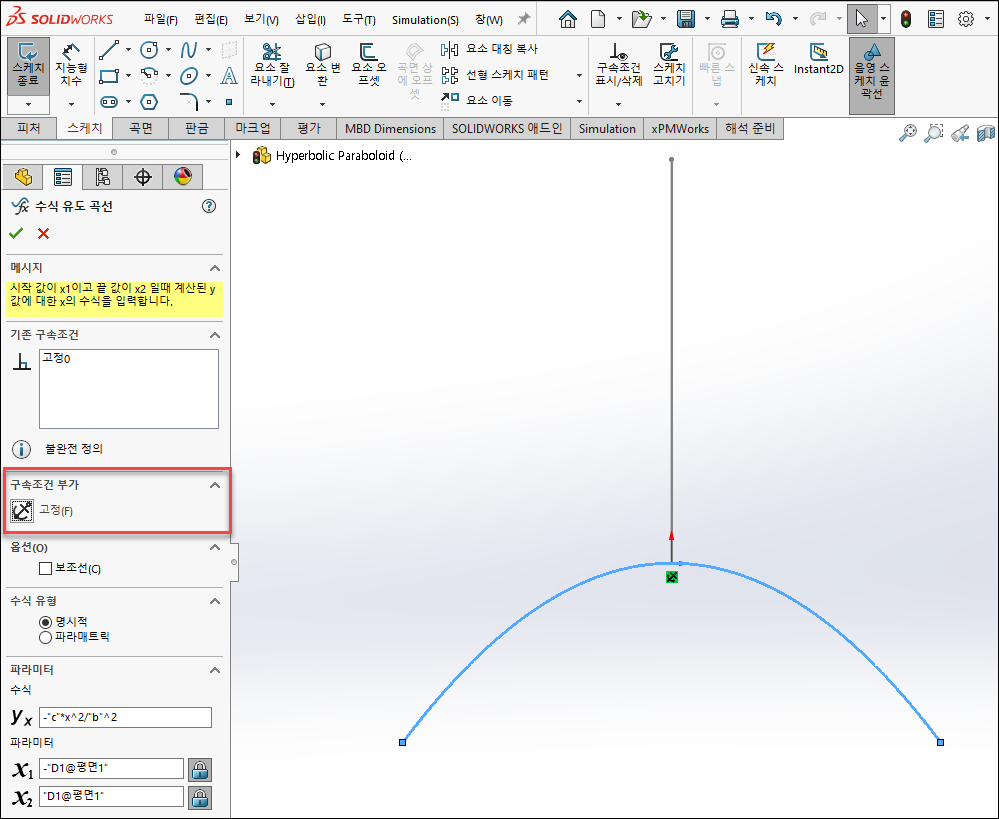
6. 평면1(x=3)에 스케치 작성
평면1을 선택 후 스케치 > 수식 유도 곡선 클릭
6.1 방정식 작성
에서 x=3인 경우 z2=3222−y232이고 변수로 변환하면 z=c×(32a2−y2b2) 입니다.
또 z=c×(32a2−y2b2) 을 SOLIDWORKS 수식으로 나타내면 z="c"*("D1@평면1"^2/"a"^2-x^2/"b"^2) 입니다.
32 자리에 "D1@평면1"이 들어왔는데 이 이유는 x=3="D1@평면1"입니다.
이 수식을 수식 유도 곡선의 수식 란에 작성합니다.
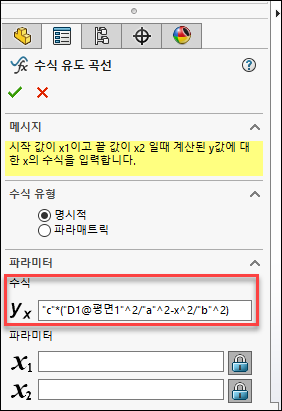
6.2 파라미터 작성
위의 4.3에서 작성했던 x의 범위를 기입합니다.
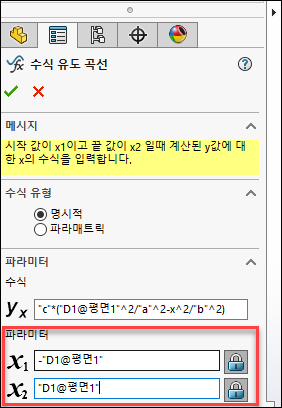
6.3 수식 유도 곡선 작성
수식과 파라미터를 모두 작성 후 확인을 누르고 스케치 선을 클릭 후 고정 구속조건을 부가합니다.
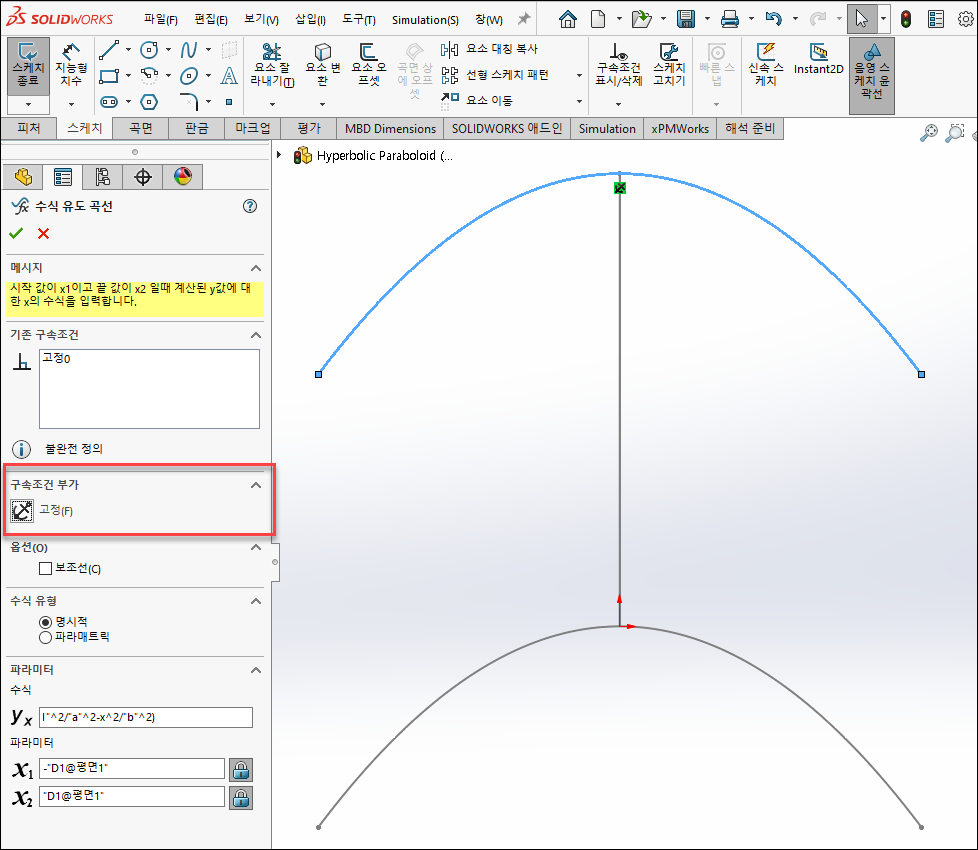
7. x=-3인 평면 만들기
곡선의 스케치 끝점과 YZ평면을 ctrl로 잡고 기준면을 선택해 평면을 만듭니다.
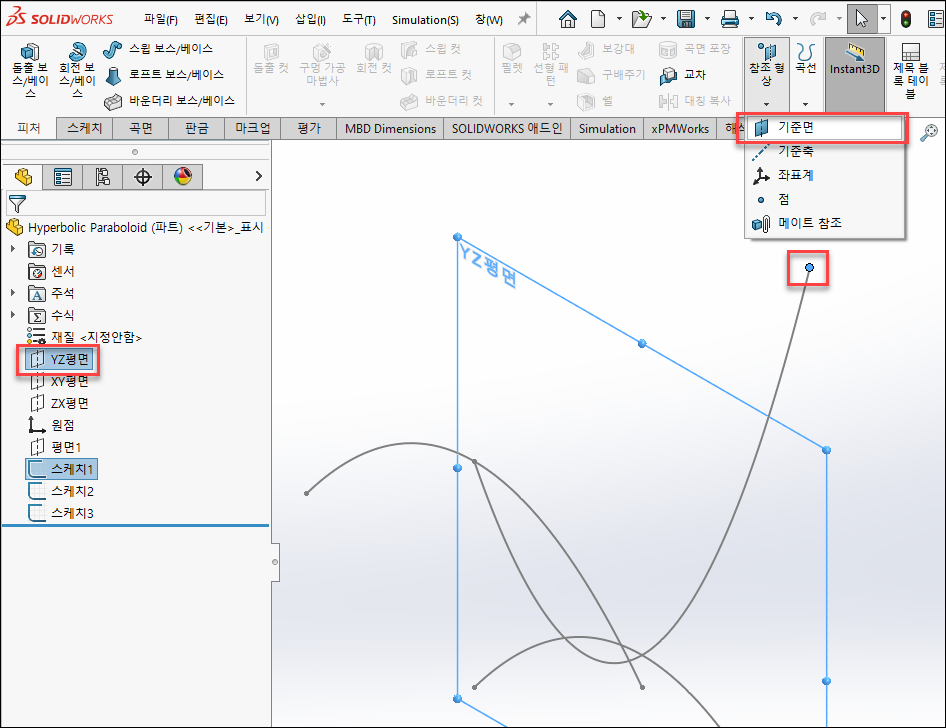
8. 평면2(x=-3)에 수식 유도 곡선 작성
위의 6.1 ~ 6.3에서 작성한 수식과 파라미터를 그대로 사용합니다.
스케치도 고정합니다.
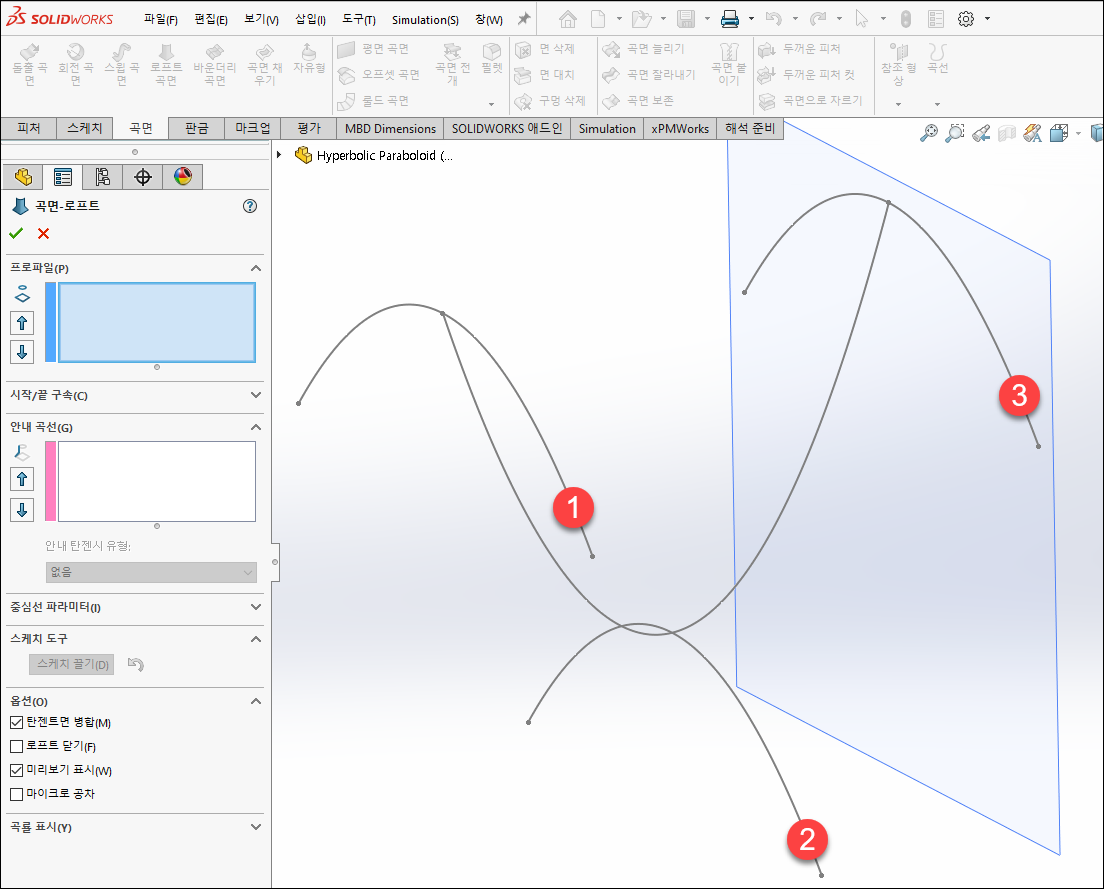
9. 곡면 생성
Command Manager에서 곡면 > 로프트 곡면을 선택합니다.
아래의 번호의 순서와 똑같이 스케치선을 클릭 합니다.
(클릭 시 마우스 위치도 동일하게 합니다.)
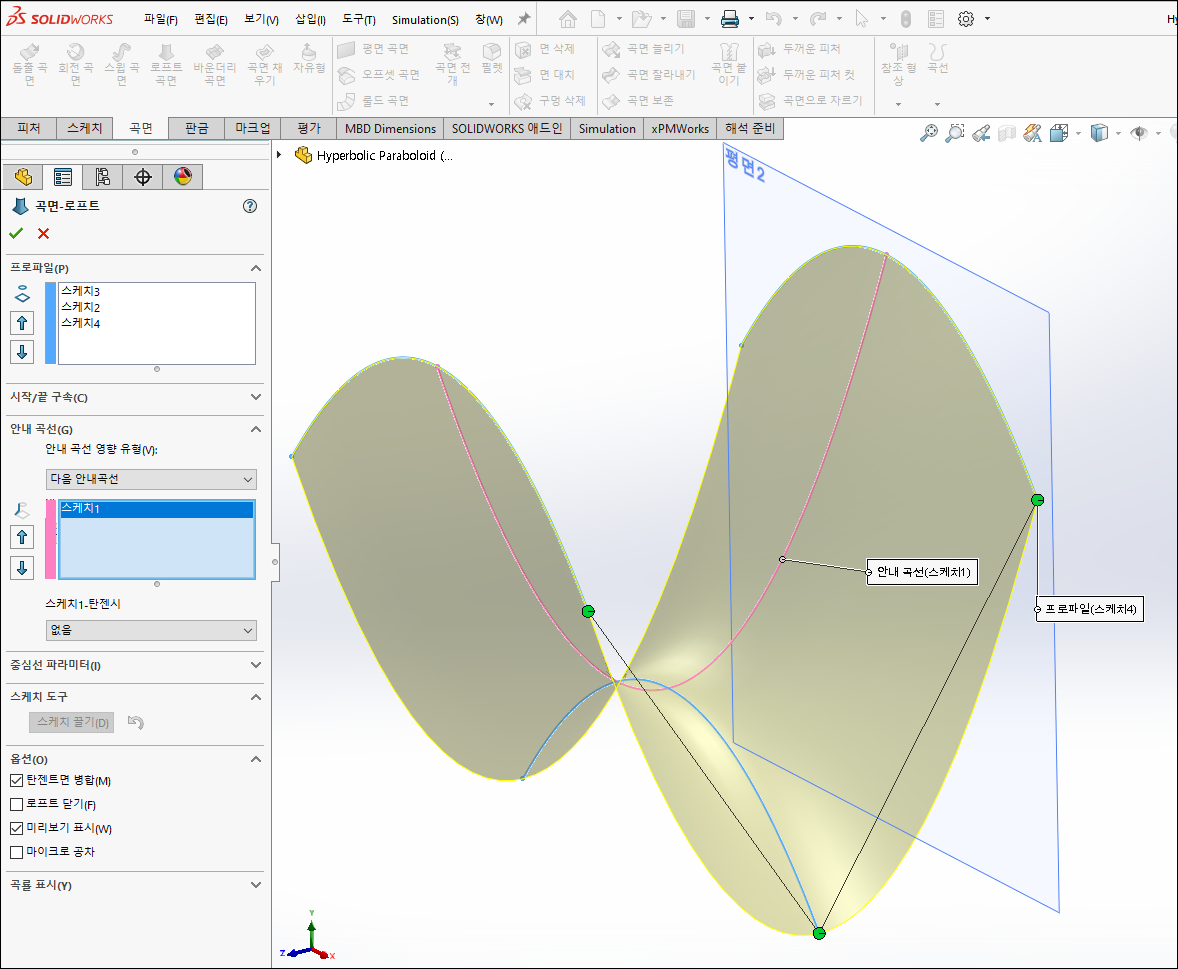
9.1 곡면 생성 화면(완성)
프로파일과 안내 곡선을 모두 선택 후 확인을 눌러 곡면을 생성합니다.
변수(상수a, b, c, x의 범위) 변경
앞서 작성했던 글로벌변수를 변경해서 원하는 곡면을 만들어봅니다.
FeatureManager트리에서 수식 마우스 오른클릭 > 수식관리
a=30, b=40, D1@평면1=160으로 변경 후 확인
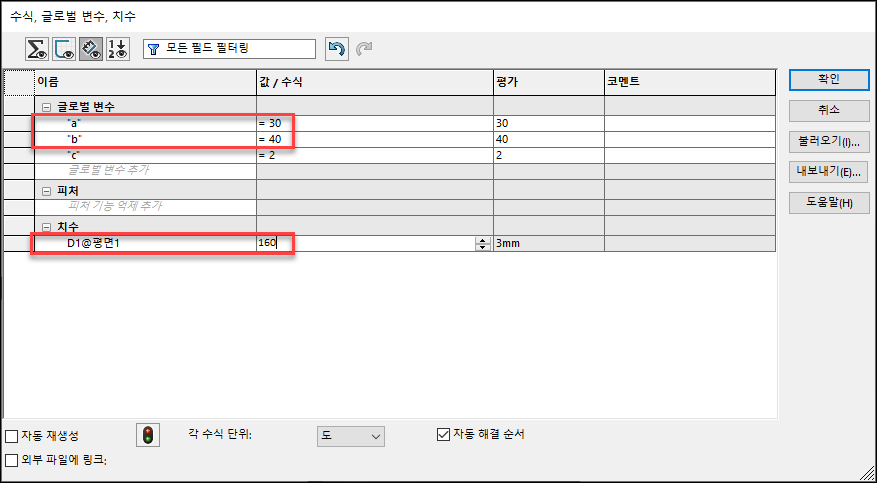
오류 찾기가 나와도 닫기를 누르고 강제 재생성(Ctrl+Q)를 누릅니다.
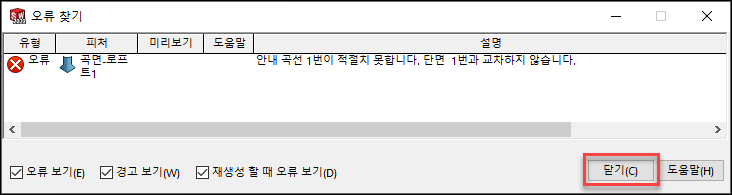
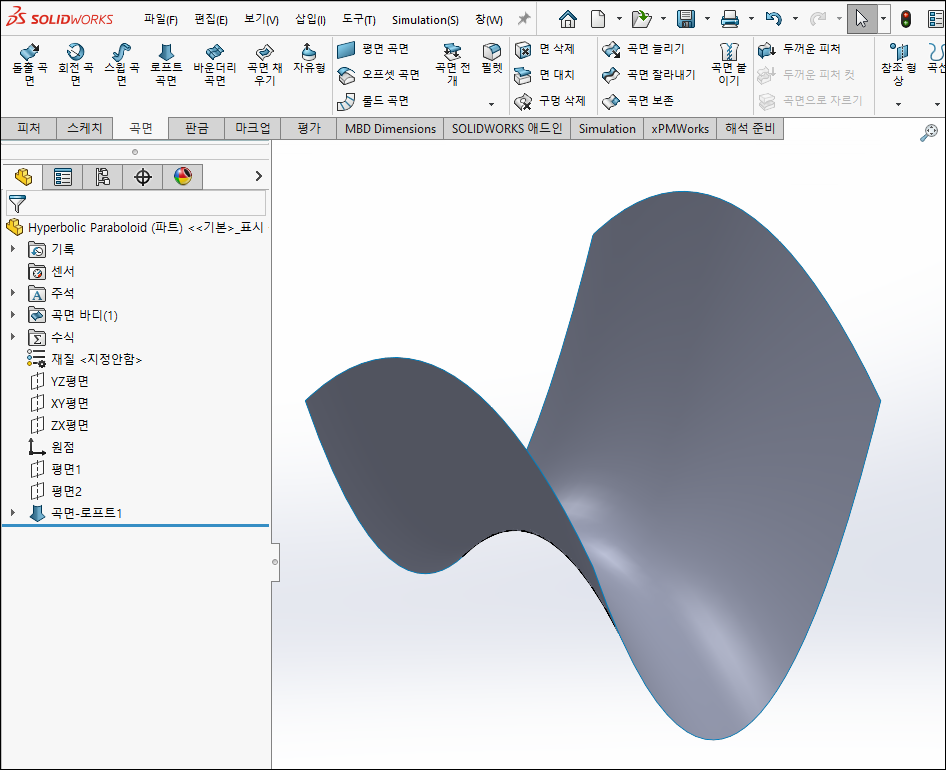
10. 모델링 확인
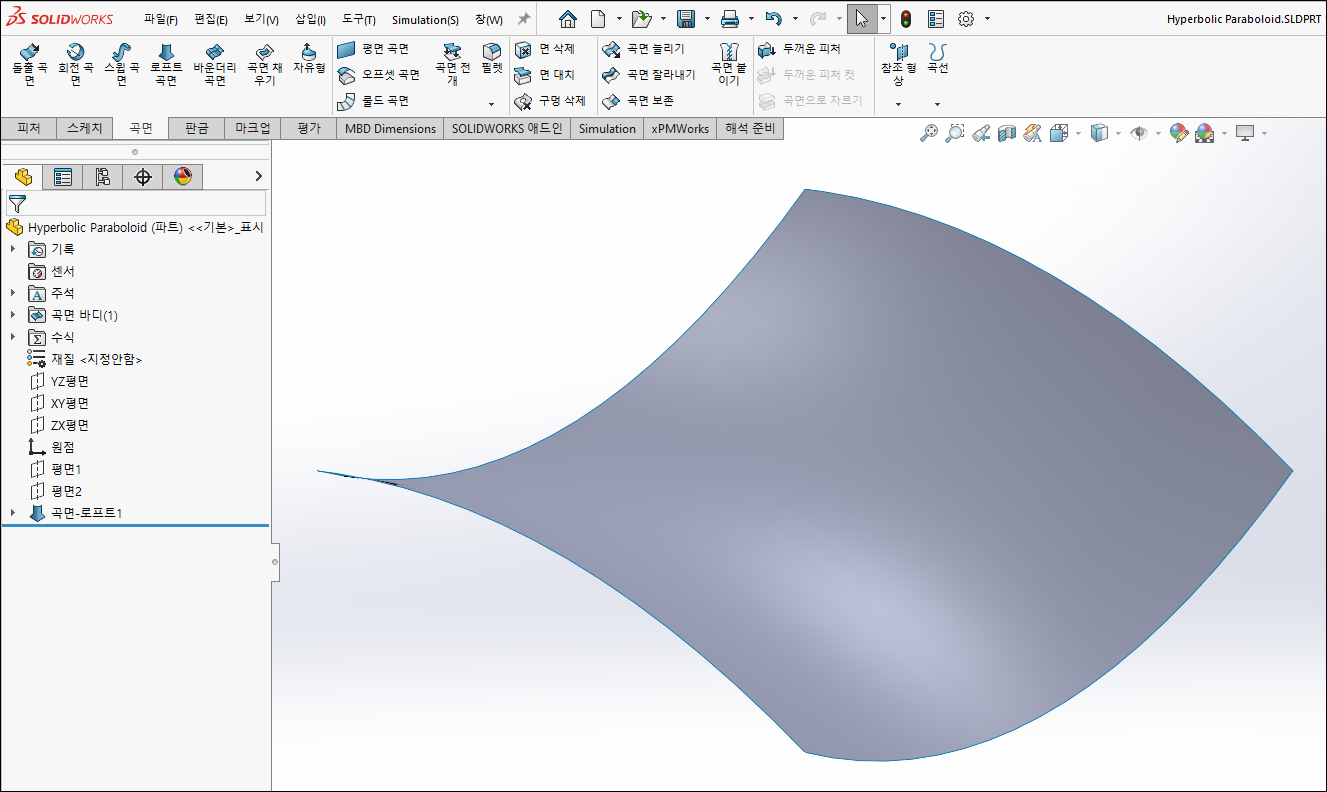
11. Pringles 모양 만들어 보기
XY평면에 스케치 > 원 작성 ,원의 크기는 x의 좌표 범위("D1@평면1"=160)보다 작게 작성
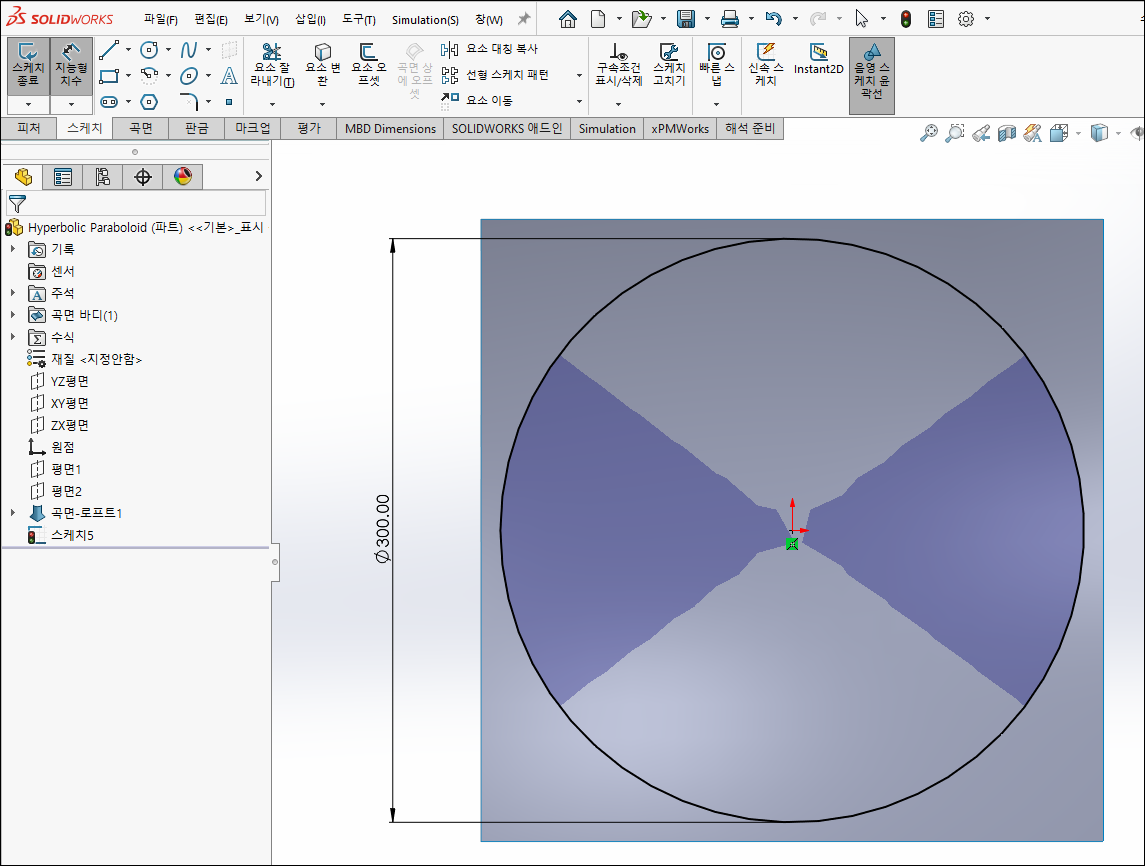
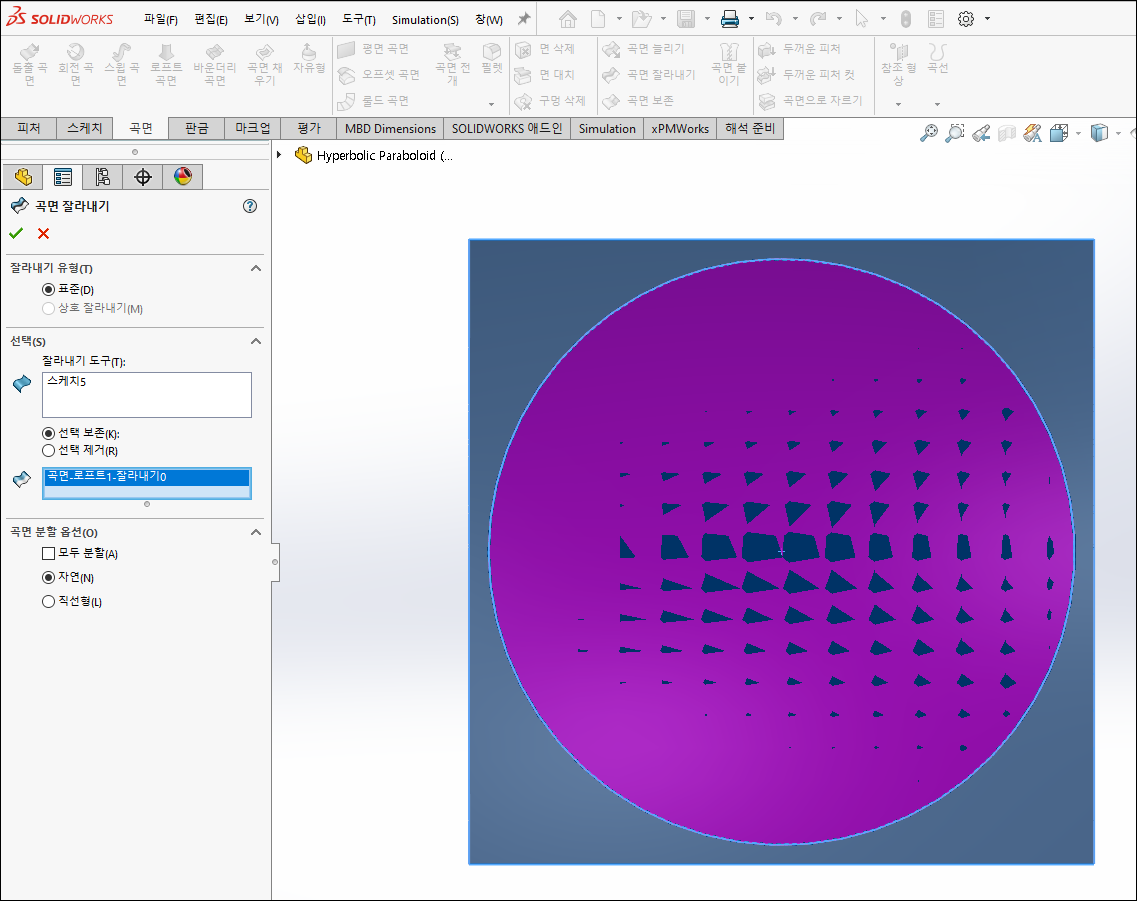
11.1 곡면 잘라내기
CommandManager에서 곡면 > 곡면 잘라내기 선택
보존할 면으로 중심 면을 선택 후 확인을 클릭합니다.
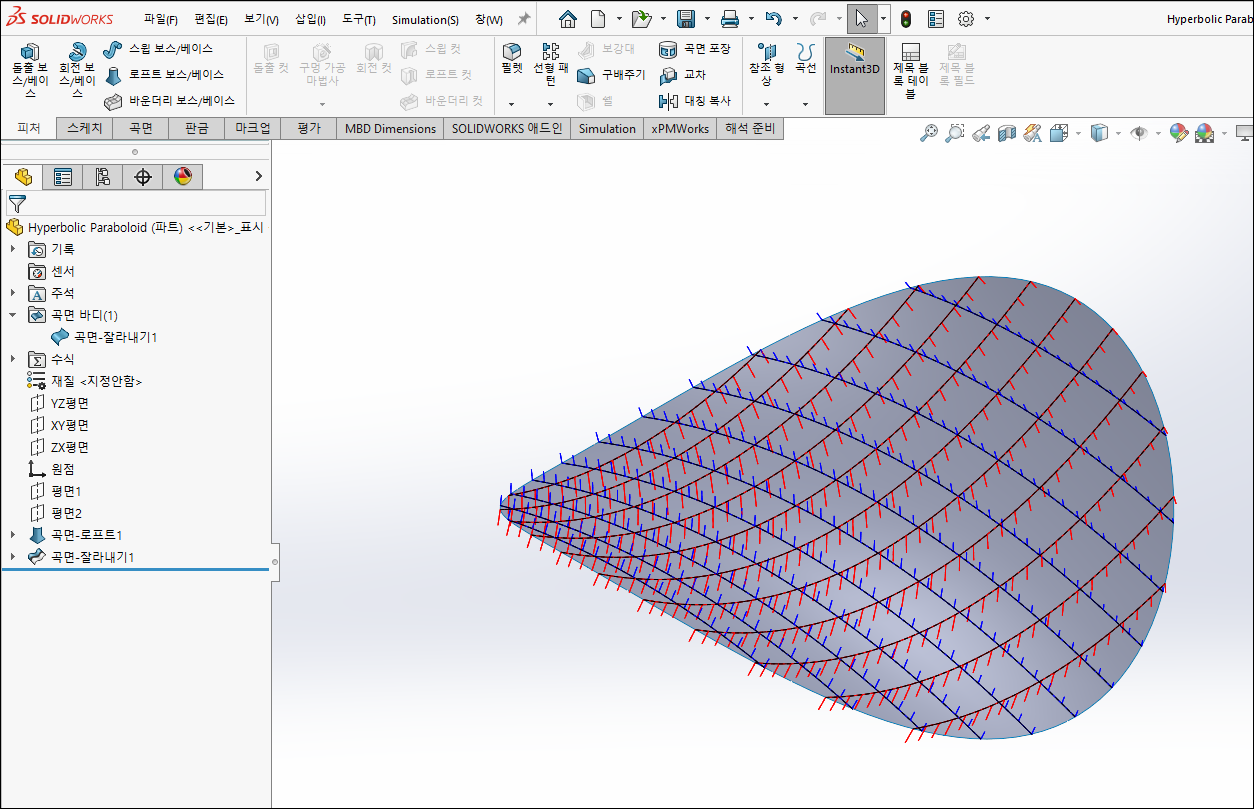
12. 완성


 Hyperbolic Paraboloid.SLDPRT (188.8 KB)
Hyperbolic Paraboloid.SLDPRT (188.8 KB)
